Min forskning
Mitt forskningsområde är prediktionsreglering (MPC) och dess applikation inom flygindustrin. Jag har valt att fokusera på den övergripande formuleringen av optimeringsproblemet som är basen i MPC reglering samt på dess teoretiska egenskaper. De egenskaper jag tittar närmare på är stabilitet och robusthet.
Stabilitet
MPC reglering är en olinjär reglerstrategi och hos dessa är stabilitet många gånger svårare att garantera. För MPC gäller det att kunna garantera att det underliggande optimeringsproblemet alltid har en lösning och att den lösningen alltid stabiliserar det slutna systemet. Detta görs oftast genom att lägga till så kallade stabiliserande bivillkor i optimeringsproblemet, men dessa bivillkor är formulerade för en fix referenssignal (oftast noll). Väldigt lite forksning finns gjord för hur dessa bivillkor ska formuleras då systemet har en varierande referenssignal.
En del i min forskning har gått ut på att ta fram en ny formulering av de stabiliserande bivillkoren så att stabilitet kan garanteras för godtyckiga referenssignaler. Med min formulering blir optimeringsproblemet enklare att lösa jämfört med andra metoder som också hanterar godtyckliga referenssignaler.
De artiklar som behandlar detta ämne är Reference Tracking MPC using Dynamic Terminal Set Transformation och Reference Tracking MPC using Terminal Set Scaling.
Ytterligare en problemställning är hur man garanterar stabilitet när systemet är olinjärt. Detta komplicerar problemet ytterligare och i de fleseta fall finns inga praktiska lösningar på detta. Jag har i artikeln Nonlinear Model Predictive Control using Feedback Linearization and Local Inner Convex Constraint Approximations tagit fram en metod som bygger på att man via en inre reglerloop linjäriserar de ursprungliga systemet (så kallad exakt linjärisering). Då hamnar systemets olinjäriteter istället på bivillkoren och jag löser det genom att göra en serie lokala linjära (konvexa) approximationer av bivillkoren. Detta medför att metoden kan garantera stabilitet och beräkningskomlpexiteten blir rimlig.
Robusthet
I den senare delen av min forskning har jag nu börjat fokusera på problemställningen om vad som händer när ens modell av flygplanet inte stämmer. Detta medför att prediktionen av flygplanets respons blir felaktig och vi kan inte längre garantera att flygplanet inte bryter mot några begränsningar.
Det klassiska sättet inom MPC att ta hänsyn till detta är att ta till en extra marginal till alla begränsingar så att man vet att flygplanet inte bryter mot någon begränsning oavsett modellfel eller störningar. Detta angreppsätt är inte lämpligt för problem inom flygindustrin som jag studerar så någon annan approach är önskvärd. Grundidén jag undersöker är om det går att använda en observatör för att skatta modellfel och störning och sedan använda den informationen i regulatorn. Detta är det normala sättet att införa integralverkan i MPC men jag studerar mer vad som kan göras gällande stabilitetsgarantier och prestanda för denna typ av formuleringar.

Industridoktorand i reglerteknik
- Telefon:
- 013-281892
- E-post:
- Adress:
- Institutionen för systemteknik
- Linköping universitet
- 581 83 Linköping
- Besöksadress:
- Campus valla
- Hus B
- Rum 2A:538 (i A-korridoren på entreplan mellan ingång 27 och 29)
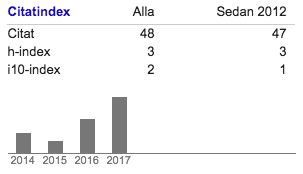
Citeringar
Informationsansvarig: Daniel Simon
Senast uppdaterad: 2014-12-02
 LiU Homepage
LiU Homepage
